注:
(1)题目表述可能与原卷有出入,表意应当没有区别。
(2)本文不作为严格的答题标准或评分标准,仅供说明可能的解题思路。
(3)函数图像全部采用计算机生成图像,确保准确。
(4)本文完全原创,但转载不必注明出处,请尽情转发给有需要的人。
(5)后续可以补充完整全卷所有题目。
(6)如发现任何错误,敬请立即向笔者指出。
18题
$$ f(x) = \ln(1+x) - x + \frac{1}{2}x^2 - kx^3, \quad 0 < k < \frac{1}{3} $$(1) 证明:$f(x)$ 在 $(0, +\infty)$ 上存在唯一极值点和唯一零点;
(2) 设(1)中的极值点和零点分别为 $x_1$ 和 $x_2$。
(i) 设 $g(t) = f(x_1 + t) - f(x_1 - t)$,证明:$g(t)$ 在 $(0, x_1)$ 上单调递减;
(ii) 比较 $2x_1$ 与 $x_2$ 的大小,并证明。
解答: (1)求导(函数定义域均为$(0,+\infty)$):
$$ f'(x) = \frac{1}{1+x} - 1 + x - 3kx^2 = x^2\left(\frac{1}{1+x} - 3k\right) $$$$ f''(x) = -\frac{1}{(1+x)^2} + 1 - 6kx $$$$ f'''(x) = \frac{2}{(1+x)^3} - 6k $$由条件
$$ f'(x_1) = 0 $$解得
$$ x_1 = \frac{1}{3k} - 1 $$作图:(取$k = \frac{1}{6}$时作图)
图1: $f'''(x)$
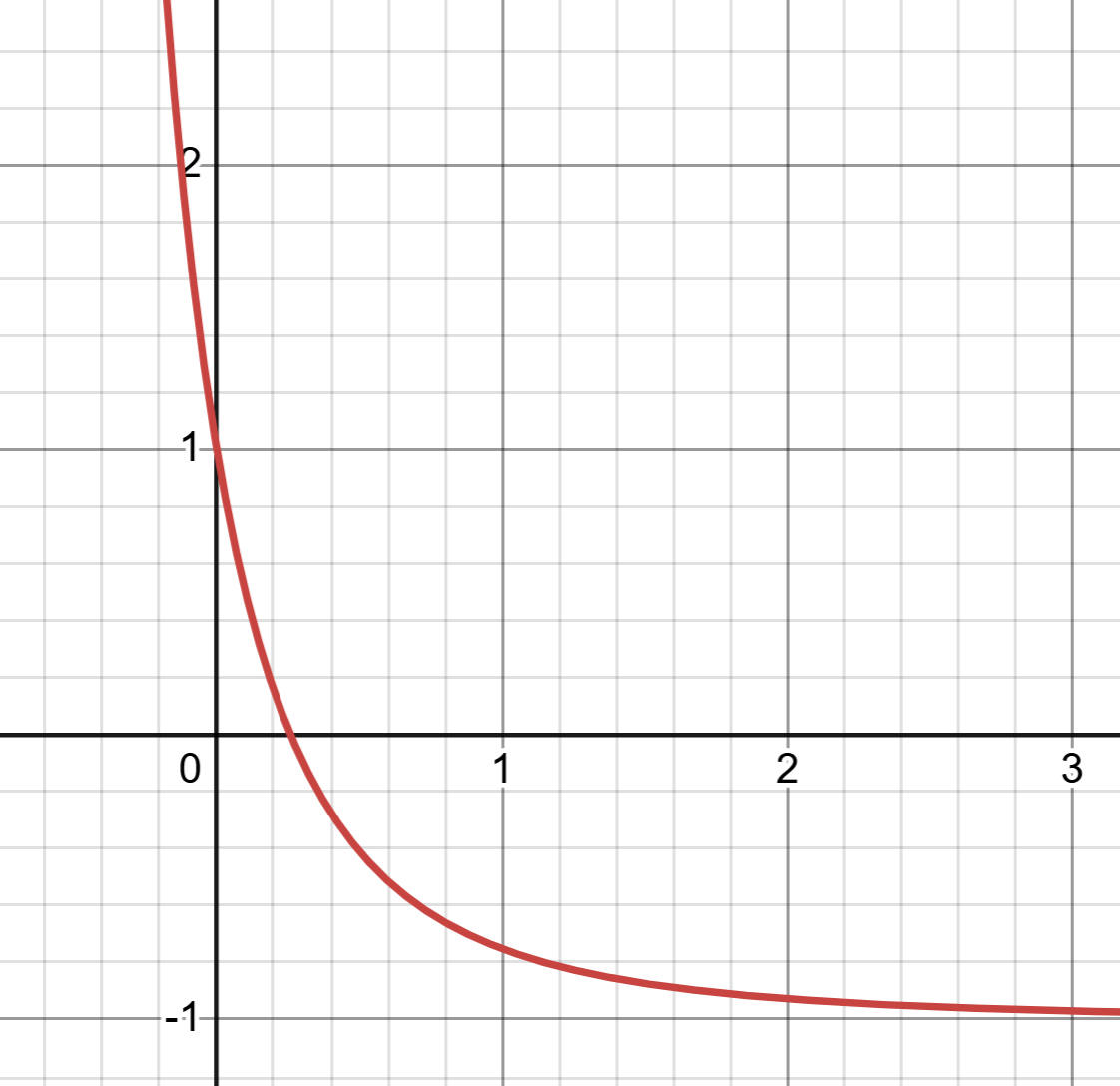
图2: $f''(x)$
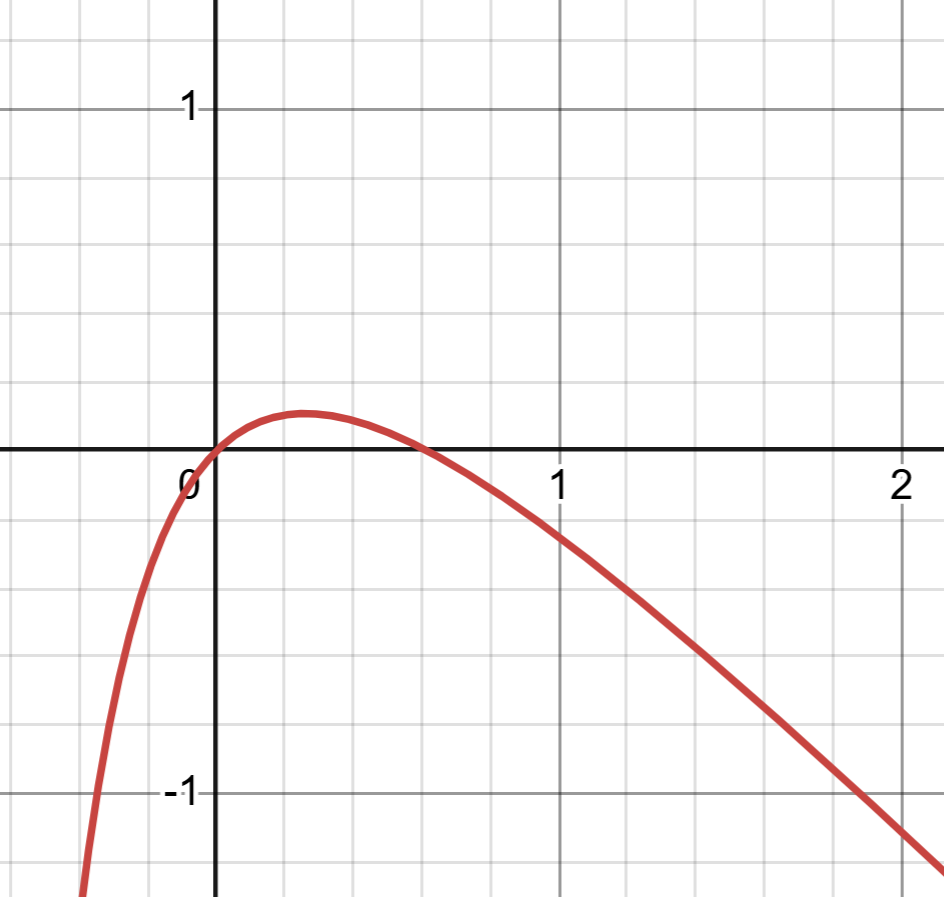
图3: $f'(x)$
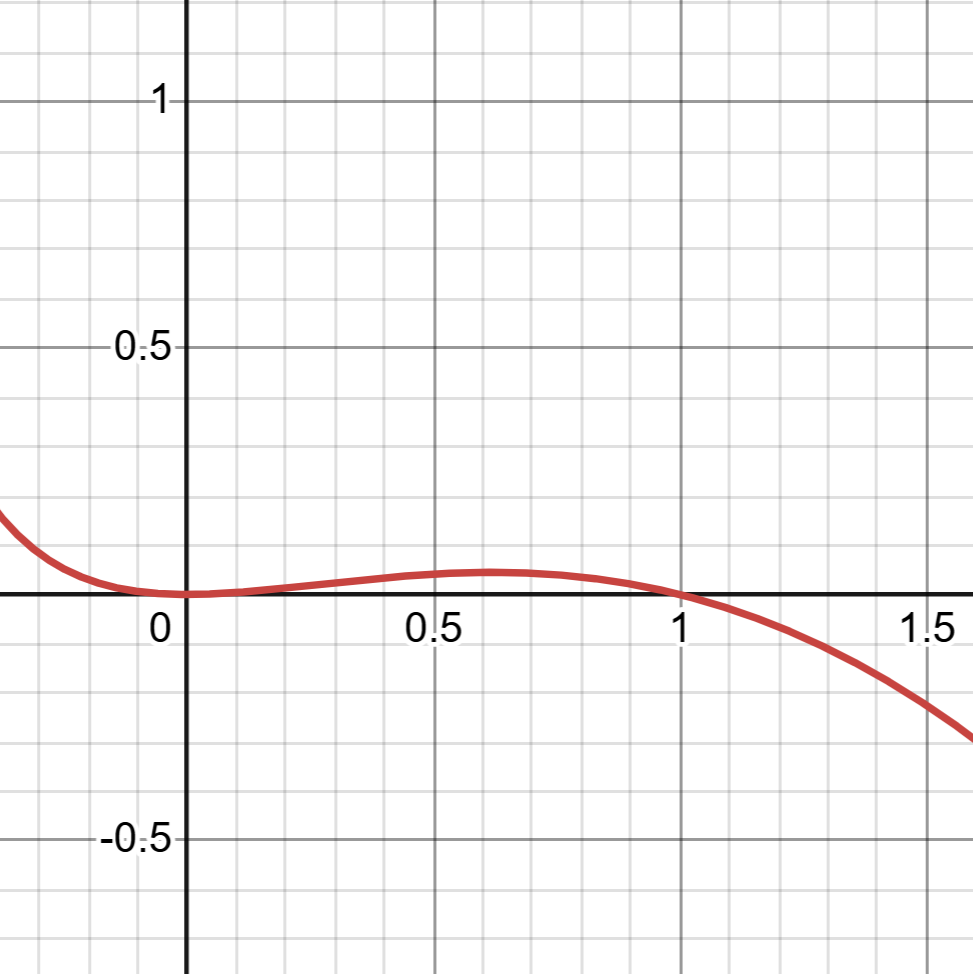
图4: $f(x)$

得到$f(x)$在区间$(0,x_1)$上单调递增,在区间$(x_1, +\infty)$上单调递减(当然,需要用不等式严格说明),又$f(0) = 0$,故必存在零点$x_2 > x_1$.
(2)
(i)
$$ g'(t) = f'(x_1+t) + f'(x_1-t) $$$$ = (x_1+t)^2\left(\frac{1}{1+x_1+t}-3k\right) + (x_1-t)^2\left(\frac{1}{1+x_1-t}-3k\right) $$$$ = \left(\frac{1-3k+3kt}{3k}\right)^2 \frac{3k-3k(1+3kt)}{1+3kt} + \left(\frac{1-3k-3kt}{3k}\right)^2 \frac{3k-3k(1-3kt)}{1-3kt} $$$$ = \frac{1}{3k}\left(\frac{(1-3k-3kt)^2}{1-3kt} - \frac{(1-3k+3kt)^2}{1+3kt}\right) $$(注:此处若将$k$用$x_1$表示也可以,注意取值范围即可)
构造辅助函数
$$ h(u) = \frac{(u-3k)^2}{u} = u + \frac{9k^2}{u} - 6k,\quad u>0 $$易知$h(u)$在$u=3k$处取到最小值0,在区间$(0,3k)$单调递减,在区间$(3k,+\infty)$单调递增. 再取
$$ u_1 = 1+3kt,\quad u_2 = 1-3kt $$(相信各位可以看出来了,不过我还是写完整),由
$$ 0 < t < x_1 = \frac{1}{3k}-1 $$得
$$ 0 < 3k < u_2 < u_1 $$故
$$ g'(t) = \frac{1}{3k}(h(u_2)-h(u_1))<0 $$即$g(t)$在区间$(0,x_1)$上单调递减.
(ii)
易知
$$ g(0) = 0,\quad g(x_1)=f(2x_1)<0=f(x_2) $$由$f(x)$的单调性可得
$$ 2x_1 < x_2 $$19题
甲乙二人打乒乓球,每个球胜者得1分,负者得0分。设每个球甲胜概率为 $p\,(½
(2)若 $\displaystyle\frac{p_4-p_3}{q_4-q_3}=4$,求 $p$。
(3)证明:对任意正整数 $m$,有
解答:
先来梳理题意。题意中甲和乙除了获胜概率不同外,地位完全对称。打完 $n$ 个球后所有可能的情况只有 $n+1$ 种,即甲 $k$ 分乙 $n-k$ 分,不妨简记为“甲 $k$ 乙 $n-k$”,另记“甲比乙至少多得2分”为“甲超”。
下面给出完整的四个表格,分别对应 $n=2m$与$n=2m+1$ 的“甲超”与“乙超”情形。
当 $n=2m$ 时(共 $2m$ 票)
甲超(甲票数 > 乙票数,共 $m$ 种):
| 序号 | 甲 得票数 | 乙 得票数 |
|---|---|---|
| 1 | $2m$ | 0 |
| 2 | $2m-1$ | 1 |
| … | … | … |
| $m$ | $m+1$ | $m-1$ |
乙超(乙票数 > 甲票数,共 $m$ 种):
| 序号 | 乙 得票数 | 甲 得票数 |
|---|---|---|
| 1 | $2m$ | 0 |
| 2 | $2m-1$ | 1 |
| … | … | … |
| $m$ | $m+1$ | $m-1$ |
当 $n=2m+1$ 时(共 $2m+1$ 票)
甲超(甲票数 > 乙票数,共 $m$ 种):
| 序号 | 甲 得票数 | 乙 得票数 |
|---|---|---|
| 1 | $2m+1$ | 0 |
| 2 | $2m$ | 1 |
| … | … | … |
| $m$ | $m+2$ | $m-1$ |
乙超(乙票数 > 甲票数,共 $m$ 种):
| 序号 | 乙 得票数 | 甲 得票数 |
|---|---|---|
| 1 | $2m+1$ | 0 |
| 2 | $2m$ | 1 |
| … | … | … |
| $m$ | $m+2$ | $m-1$ |
据此可写出 $p_n$ 和 $q_n$ 的通项,然而在本题中没必要这样做。
(1) 易知:
$$ p_3 = p^3,\quad p_4 = p^4 + \binom{4}{1} p^3 q = p^4 + 4p^3 q = p^3(4 - 3p) $$(2) 由对称性即得:
$$ q_3 = q^3,\quad q_4 = q^4 + \binom{4}{1} q^3 p = q^4 + 4q^3 p = q^3(4 - 3q) $$因此:
$$ \frac{p_4 - p_3}{q_4 - q_3} = \frac{3(p^3 - p^4)}{3(q^3 - q^4)} = \frac{p^3(1 - p)}{q^3(1 - q)} = \frac{p^3(1 - p)}{(1 - p)^3 p} = \left(\frac{p}{1 - p}\right)^2 = 4 $$即:
$$ p = \frac{2}{3} $$(3) 采用递推思想比较简便。
- 打完 $2m$ 球后可能情形有: I. 甲超; II. 乙超; III. 甲 $m$ 乙 $m$。
随后再打一球,II 和 III 的情形必然无法变为甲超;而 I 情形(概率为 $p_{2m}$)下,若甲胜(概率为 $p$)则必甲超;乙胜(概率为 $q$)时,除非情形正好为“甲 $m+1$ 乙 $m-1$”,否则仍甲超。
于是有递推公式:
$$ p_{2m+1} = p_{2m} p + q\left(p_{2m} - \binom{2m}{m+1} p^{m+1} q^{m-1}\right) = p_{2m} - \binom{2m}{m+1} p^{m+1} q^m $$同理分析,打完 $2m+1$ 球后可能情形有: I. 甲超; II. 甲 $m+1$ 乙 $m$; III. 甲 $m$ 乙 $m+1$; IV. 乙超。
随后再打一球,III 和 IV 情形必然无法变为甲超;I 情形(概率为 $p_{2m+1}$)必甲超;II 情形下,若甲胜(概率为 $p$),则甲超;乙胜时无甲超。
于是有递推公式:
$$ p_{2m+2} = p_{2m+1} + p \binom{2m+1}{m} p^{m+1} q^m = p_{2m} - \binom{2m}{m+1} p^{m+1} q^m + \binom{2m+1}{m} p^{m+2} q^m $$$q_n$ 的递推公式完全同理,只需将上述两递推式中 $p$ 与 $q$ 对调即得。
于是自然由 $p>q$ 有:
$$ p_{2m+1}-p_{2m} = \binom{2m}{m+1} p^{m+1} q^m < q_{2m+1}-q_{2m} = \binom{2m}{m+1} p^m q^{m+1} $$欲比较:
$$ p_{2m+2}-p_{2m} = p^{m+1} q^m\left(\binom{2m+1}{m} p - \binom{2m}{m+1}\right) $$与
$$ q_{2m+2}-q_{2m} = p^m q^{m+1}\left(\binom{2m+1}{m} q - \binom{2m}{m+1}\right) $$只需比较:
$$ \binom{2m+1}{m} p^2 - \binom{2m}{m+1} p \quad\text{与}\quad \binom{2m+1}{m} q^2 - \binom{2m}{m+1} q $$由 $p+q=1$,即比较:
$$ \binom{2m+1}{m}(p^2-q^2) = \binom{2m+1}{m}(p-q) \quad\text{与}\quad \binom{2m}{m+1}(p-q) $$由:
$$ \frac{\binom{2m}{m+1}}{\binom{2m+1}{m}} = \frac{m}{2m+1} < 1 $$得到:
$$ p_{2m+2}-p_{2m} > q_{2m+2}-q_{2m} $$综合以上,有结论:
$$ p_{2m+1}-q_{2m+1} < p_{2m}-q_{2m} < p_{2m+2}-q_{2m+2} $$直观理解:因为甲水平比乙高,所以随着比赛局数增加,甲超的可能性与乙超的可能性的差值会越来越大,符合经验。